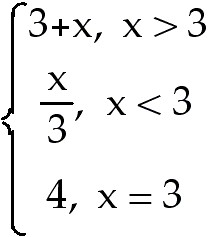Bucks County Community College Distance Learning Calculus |
||||||||
|---|---|---|---|---|---|---|---|---|
Instructor: Mrs. Fitt |
||||||||
|
Practice for Midterm
Find the average rate of change of the function over the given interval. Round to nearest thousandth, if necessary. 1) y = 4 Complete the table for the function and find the indicated limit. 2) If f(x) =
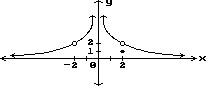
3) Use the graph to estimate the limit of the function.
4) 5) Evaluate the limit.
8) Write the definition of the derivative. Find the derivative of the given function at the given point using the definition. f(x) = 3 9) Find the limit, if it exists. Let f(x) =
11) Find the x-values where a) the function is discontinuous b) the function is not differentiable.
Find the intervals on which the function is continuous. 12) y = 13) y = 14. Find the equation for the tangent to the curve at the given point. f(x) = 5x2 + x; (-4, 76) Solve the problem. 15. Find the points where the graph of the function have horizontal tangents. f(x) = 16. Find an equation of the tangent to the curve f(x) = 17. Use the definition to find the function's derivative. Then evaluate the derivative at the indicated point. g(x) = 3x2 - 4x, 18. Find the derivative. f(x) = 4x4 + 3x3 + 6 19. Find an equation for the line tangent to given curve at the indicated point. y = x - 20. The function s = f(t) gives the position of a body moving on a coordinate line, with s in meters and t in seconds, for the given time interval. Use s(t) to find the indicated quantities. s = - Find the body's velocity and acceleration at the end of the time interval. 21. A rock is thrown vertically upward from the surface of an airless planet. It reaches a height of 22. Find 23. y = 24 y = Find the derivative. 26 y = 27. r = 18 - 28.Find the indicated derivative. Find 29. Find the derivative of the function. y = 30. r = 31. f(θ) = sin 32. y = 33. q = cos 34. h(x) = 35. y = 36. Find 36. y = 38. x3 + 3x2y + y3 = 8 39. y 40. Find the slope at the indicated point on the given curve.
Find the related rate equation. 41) Suppose that the radius r and volume V = 42. A product sells by word of mouth. The company that produces the product has noticed that revenue from sales is given by 43.The radius of a right circular cylinder is increasing at the rate of 44. Find the absolute extreme values of each function on the interval. F(x) = 3 4 5. Find the extreme values of the function and where they occur. y = 46. Find each critical point and determine if it is a max, min or neither y = 47. y = Use analytic methods to find the intervals on which the function is increasing, decreasing, concave up, and concave down. Also, locate and identify the local extrema and inflection points. 48. y = Click here to see the answers.
|
|||||||
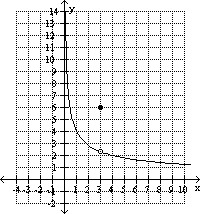 (a)
(a) 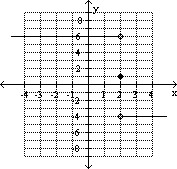 Find
Find