|
Test |
Series |
Convergence or divergence |
Comments |
|
nth term test for divergence |
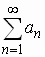
|
Diverges if 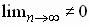 |
Use this test first if divergence is suspected. However, test is
inconclusive if 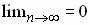 , so try another test. , so try another test. |
|
Geometric series |
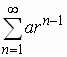
|
(a) Converges if | r | < 1
(b) Diverges if 
|
The first term is a and each term is a multiple, r of the
previous term. Also useful for comparison tests if the nth term of
a series is similar in magnitude to r n-1. If
|r|< 1, 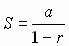 . . |
|
p-series |
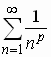
|
(a) Converges if p > 1
(b) Diverges if 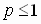 |
Useful for comparison tests if the nth term of a series is similar
in magnitude to 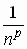 . . |
|
Integral Test |
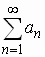
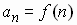
|
(a) Converges if 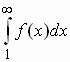 converges converges
(b) Diverges if 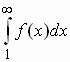 diverges diverges |
The function É obtained from 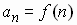 must
be continuous, positive, decreasing. Use if you can integrate the
function. must
be continuous, positive, decreasing. Use if you can integrate the
function. |
|
Individual Comparison
Test |
Given 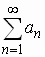
compare to 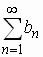 known known
to converge or to diverge |
(a) If 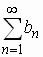 converges and converges and 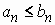 for every n then
for every n then 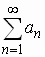 converges converges
(b) If 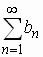 diverges and diverges and 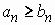 for every n then
for every n then 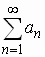 diverges diverges |
The comparison series 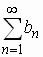 is
often a geometric series or a p-series. is
often a geometric series or a p-series.
To show convergence, you must find a series known to converge that is
greater than the given series.
To show divergence, you must find a series known to diverge that is
smaller than the given series.
Hints: ln n < n and |sin n | and |cos n|
are always less than or equal to 1. |
|
Limit Comparison
Test |
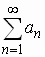 , ,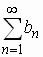
|
(a) If 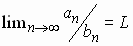 for some positive real number L then
both series converge or both diverge. for some positive real number L then
both series converge or both diverge.
(b) If the limit is 0 and bn is known to converge, then an
converges too.
(c) If the limit is • and bn is
known to diverge, an diverges too. |
To find bn in the limit comparison test, consider only the
terms in an that have the greatest effect on the magnitude. Use
LíHopitalís rule when needed. This often is helpful when ln n appears. |
|
Ratio
Test |
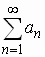
|
If 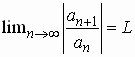 , the series , the series
(a) converges (absolutely) if L <1.
(b) diverges if L >1 (or • ) |
Inconclusive if L = 1. Useful if an involves factorials or
nth powers. If all terms are positive then absolute value sign may be
disregarded.
(n+1)!/n! = n+1
2n+1/2n = 2
n +1 term for (2n)! is (2(n+1))! = (2n + 2)! |
|
Root Test |
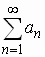
|
If 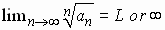 , the series , the series
(a) converges (absolutely) if L <1.
(b) diverges if L >1 (or • )
|
Inconclusive if L = 1. Useful if nth term involves nth powers. 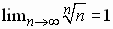 |
|
Alternating series
Test |
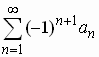
|
Converges if
(a) 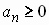
(b)  for every n >M for every n >M
(c) 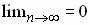 |
Applies only to alternating series. Series diverges if any one of the
conditions is not met. Exponent on numeric factor may be n or n+1
depending on whether the terms are negative for n odd or even. |
|
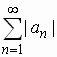
|
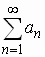
|
If 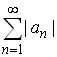 converges then converges then 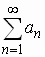 converges converges
If a series converges absolutely, then it converges. A series that
converges but does not converge absolutely is called conditionally
convergent. |
Useful for series containing both positive and negative terms that do
not alternate. Use for series with trig functions. This is also useful
when you know the non-negative series converges. Adding some negative
terms will only make the series converge more quickly. Note the converse
to this is not true. For example, the alternating harmonic series
converges by the alternating series test but the nonnegative harmonic
series diverges. |
