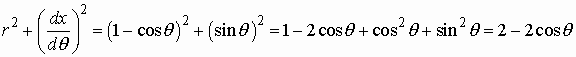1. Convert the polar
equation to rectangular form. 
2. Convert the rectangular
equation to polar form. 
.
3. Find dy/dx and find the
points of horizontal tangents and vertical to the graph of 
[0,2p ]
4. Find the slope of the
line tangent to the curve 
5.Find the points of horizontal tangency
(if any) to the polar curve 
.
6. Find the area of the
region inside 
and outside 
Answers
1. 
. Rectangular equation is 
or 
. Completing the square gives 
or 
. circle center (0, -2) , radius 2.
2. Use 
so the polar equation is 
=0
3.
and 
and 
.
Horizontal tangents occur
where dy/dθ = 0 but dx/dθ does
not. Vertical tangents occur where dx/dθ = 0 but dy/dθ does not.
Find where dy/dθ = 0 by factoring and setting each factor equal
to 0.: 
and 
.
Find where dx/dθ = 0 by rewriting the function in terms of the
sine function. 
. The expression factors to (2sin θ
+ 1) (sin θ -1). Set
each factor equal to 0 and solve. Angles for which dx/dθ = 0 are: 
.
Note that both derivatives
are zero at p /2. Evaluate the limit as θ
approaches p /2 for the dy/dx expression. Use
So, horizontal tangents
occur at 
and
vertical tangents at
4. 
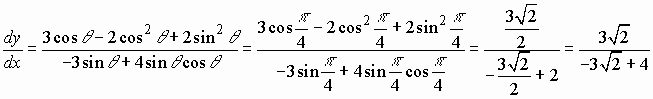
5. 
so
so 
. Horizontal
tangents occur where dy/dθ = 0 but
dx/dθ does not. Vertical tangents occur where dx/dθ = 0 but
dy/dθ does not.orizontal tangents dy/dθ = 0 when sin 2θ = 0 and
dx/dθ = 0 when cos2θ=0.
For sin 2θ = 0, 2θ = 0, p ,2p , 3p and 4p which means θ = 0, p /2,p , 3p /2 and 2p .
For cos 2θ=0, 2θ= p /2, 3p /2, 5p /2 and 7p /2. which
means that θ = p /4, 3p /4, 5p /4 and 7p /4. Since there are no angles for which both derivatives are zero,
there are horizontal tangents at θ =
0, p /2,p
, 3p /2 and 2p and vertical tangents at θ = p /4, 3p /4, 5p /4 and 7p /4.
6. Use your graphing
calculator to draw. Θ runs from -p /2 to p /2. The area is
=
=
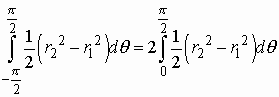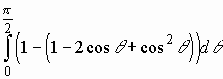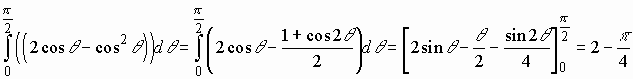
7. (skip this one) Sketch
the graph.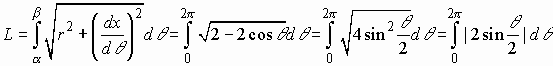 
since sin θ/2 is
positive for interval, you can ignore the absolute value signs and integrate to
.
Note that 