|
Farber Practice for Midterm test
Math 141
The questions on the midterm correspond to
questions from Test 1 and Test 2. Answers with explanations follow.
1)Find the slope of a line tangent to
the curve of  where where 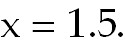
Find 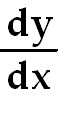 . .
2) y =
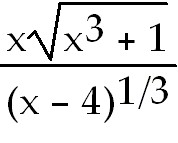
3) y =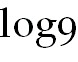 
4) y =
ln 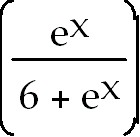
5) y =
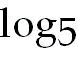 (x sin x) (x sin x)
6) y =
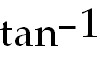 (ln 4x) (ln 4x)
7) y =
2 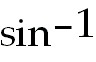 ( 4 ( 4 ) )
8)y =
ln (sinh 5x)
9) y =
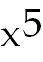 ln x - ln x -
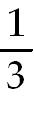 
10) y =
5 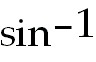 x
x
11) y =
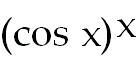
12) y =
2x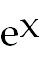 -
2 -
2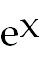
13) y =
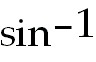 
14) y =
cosh 
Evaluate the integral
15) 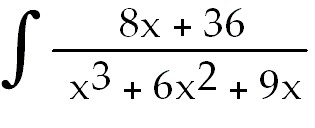 dx dx
16) 
17) 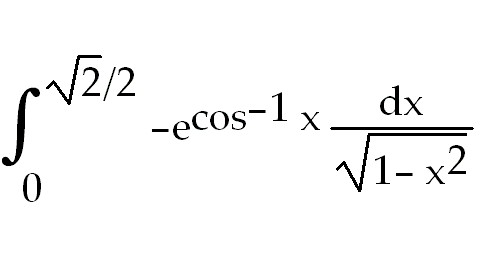
18) 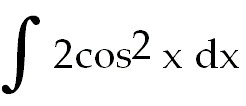
19) 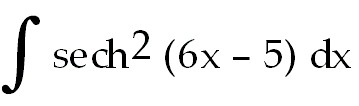
20) 
21) 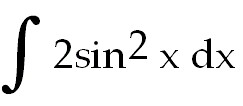
22) 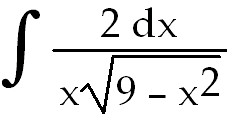
23) 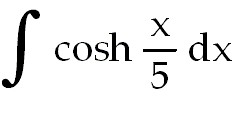
24) 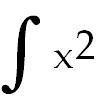 ln 3x dx ln 3x dx
25) 
26) 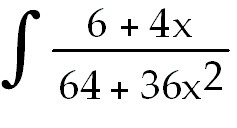 dx dx
27) 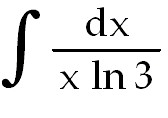
28) 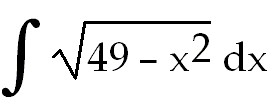
29) 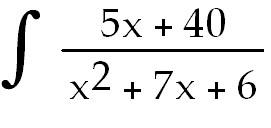 dx dx
30) 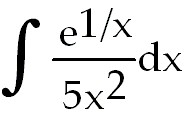
31) 
32) 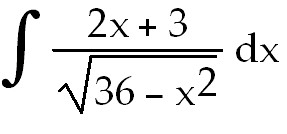
33) 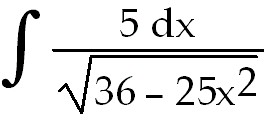
34) 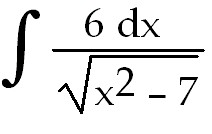
35) 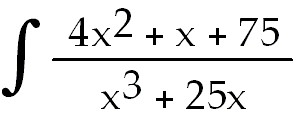 dx dx
36) 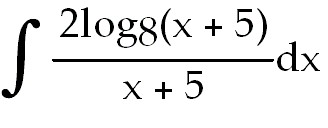
37)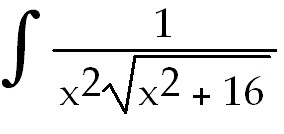 dx dx
38) 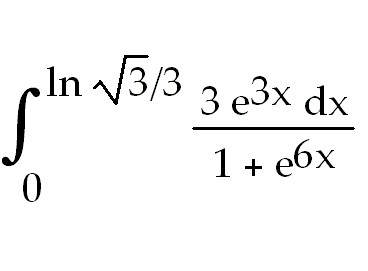
Use l'H pital's rule to find the
limit pital's rule to find the
limit
39) f(x) =
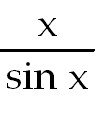 ; ; 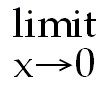 f(x). f(x).
40) 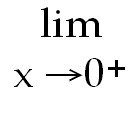 
41) 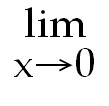 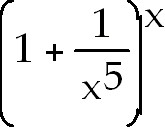
42)  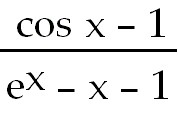
43)  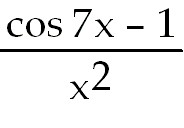
Answers with explanations.
1) 0.973. Recall that the
slope of the tangent is equal to 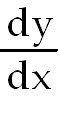 . .
2) 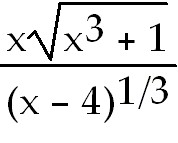 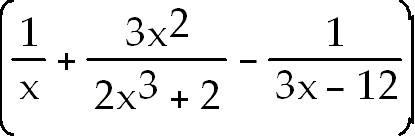 .
Take the natural log on both sides. Then differentiate with implicit differentiation.
Solve for .
Take the natural log on both sides. Then differentiate with implicit differentiation.
Solve for  . .
3) 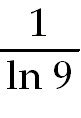 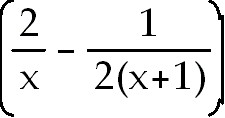 . .
Write in terms of the natural log and use rules of logs to simplify before
differentiating.
4) 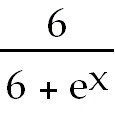 . Use rules of logs to
simplify into the difference between two logs. Then differentiate . Use rules of logs to
simplify into the difference between two logs. Then differentiate
5)  . Convert to natural log.
Remember than ln5 is a constant, so factor out . Convert to natural log.
Remember than ln5 is a constant, so factor out  .
Use the chain rule with the product rule. .
Use the chain rule with the product rule. 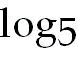 (x
sin x)= (x
sin x)=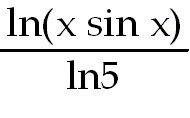 = = ln(x
sin x). There are several equivalent ways to write the answer. ln(x
sin x). There are several equivalent ways to write the answer.
6) 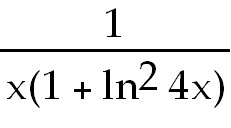 . Use the chain rule. . Use the chain rule.
7)  . Use the chain rule. . Use the chain rule.
8) 5 coth 5x. use the chain rule.
9)  - -
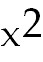 +
5 +
5 ln x ln x
10) 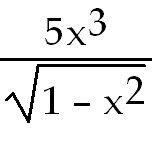 +
15 +
15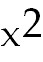 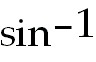 x. Use the product rule.
x. Use the product rule.
11) 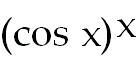 (ln cos x -
x tan x). Take the natural log on both sides. Then simplify using the laws of
logs. The right side will be (ln cos x -
x tan x). Take the natural log on both sides. Then simplify using the laws of
logs. The right side will be 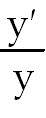 .
Solve for .
Solve for  and write in terms of
x, and write in terms of
x,
12) 2x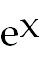
13)  . Use the chain rule. . Use the chain rule.
14) 4 sinh sinh  .
Use the chain rule. .
Use the chain rule.
15) 4 ln 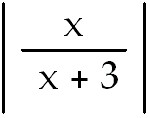 + +
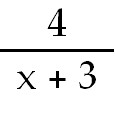 +
C. Use partial fraction decomposition. Remember you have a repeated linear
factor here so you must account for denominators for the first and second power
of this factor. +
C. Use partial fraction decomposition. Remember you have a repeated linear
factor here so you must account for denominators for the first and second power
of this factor.
16) (3z2 -
7)3/2 +
C This is a simple Calc I u-substitution.
u =
3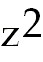 and du =
6z dz. and du =
6z dz.
17) 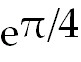 - -
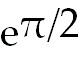 . Let u= . Let u=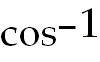 x. So du =
x. So du =
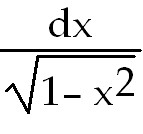
18) x +
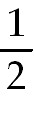 sin 2x +
C. Use the power reducing trig identity. 2 sin 2x +
C. Use the power reducing trig identity. 2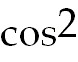 x
=
1+
cos 2x. The latter is easy to integrate. . x
=
1+
cos 2x. The latter is easy to integrate. .
19) 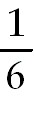 tanh ( 6x -
5) +
C. Let u =
6x-5.
Then du =
6dx. tanh ( 6x -
5) +
C. Let u =
6x-5.
Then du =
6dx.
20) 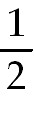 tan2 x +
C. let u=tan
x and du = tan2 x +
C. let u=tan
x and du =
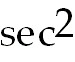 x dx or change to sines and
cosines. x dx or change to sines and
cosines.
21) x -
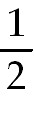 sin 2x +
C. Use the power reducing formula to rewrite 2 sin 2x +
C. Use the power reducing formula to rewrite 2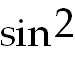 x =
1-
cos2x
x =
1-
cos2x
22) ln 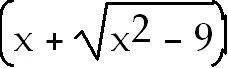 +
C. Use trig substitution with u =
3 sin θ and du =
3 cos θ. After you integrate the trig function, back substitute using a
right triangle relationship from the original substitution.
+
C. Use trig substitution with u =
3 sin θ and du =
3 cos θ. After you integrate the trig function, back substitute using a
right triangle relationship from the original substitution.
23) 5 sinh 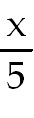 +
C. Let u = +
C. Let u =
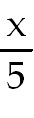 . So du =
5dx . So du =
5dx
24) 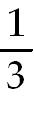 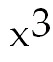 ln 3x -
ln 3x -
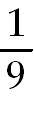 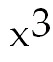 +
C. Integration by parts. u =
ln3x and dv=
+
C. Integration by parts. u =
ln3x and dv=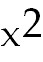 dx dx
25) -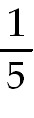 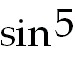 x+ x+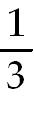
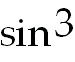 +C.
Break off a factor of cos x. Use the Pythagorean identity to rewrite +C.
Break off a factor of cos x. Use the Pythagorean identity to rewrite 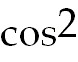 x.
You will have two terms to integrate. Both contain a power of sin x multiplied
by cos x. Use u =
sin x and du =
cos x dx. x.
You will have two terms to integrate. Both contain a power of sin x multiplied
by cos x. Use u =
sin x and du =
cos x dx.
26) 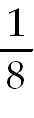 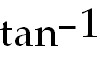
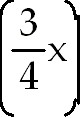 + +
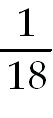 ln ln 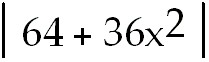 +
C. Split the numerator into two fractions. Each can be integrated separately.
+
C. Split the numerator into two fractions. Each can be integrated separately.
27) 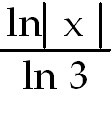 +
C. Recall that ln 3 is a constant. Move it to the left of the integral sign. +
C. Recall that ln 3 is a constant. Move it to the left of the integral sign.
28)  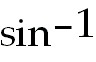
 + +
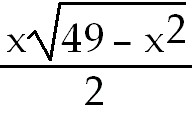 +
C. Use trig substitution. a=7
and u=x
and x=7sinθ
and dx=
7 cosθ. +
C. Use trig substitution. a=7
and u=x
and x=7sinθ
and dx=
7 cosθ.
29) ln  +
C. Use partial fractions. You can use laws of logs to simplify. +
C. Use partial fractions. You can use laws of logs to simplify.
30) -
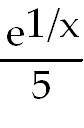 +
C. Let u = +
C. Let u =
 . Then du =
- . Then du =
-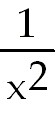 dx.
The constant dx.
The constant 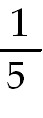 can be moved
through the integral sign. can be moved
through the integral sign.
31) (1/2)x2e2x -
(1/2)xe2x +
(1/4)e2x +
C. Use integration by parts with u =
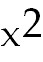 and dv = and dv =
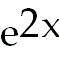 . From this result, you will have
to use integration by parts again. . From this result, you will have
to use integration by parts again.
32) -
2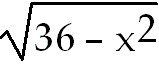 +
3 +
3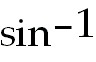  +
C. Split the numerator so you have two fractions. To integrate the first use a
simple u-substitution
of u =
36 -
+
C. Split the numerator so you have two fractions. To integrate the first use a
simple u-substitution
of u =
36 -
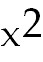 and du =
-2x
dx. For the second, use a trig substitution where x =
6 sin θ and dx =
6 cos θ dθ. and du =
-2x
dx. For the second, use a trig substitution where x =
6 sin θ and dx =
6 cos θ dθ.
33) 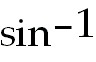  +
C. Let a =
36, u =
25x. So du =
25dx
+
C. Let a =
36, u =
25x. So du =
25dx
34) 6 ln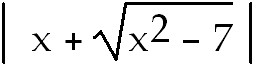 +
C. Use trig substitution with x = +
C. Use trig substitution with x =
 sec θ dx = sec θ dx =
 sec θ tan θ. Draw a
right triangle to help by back substitute. sec θ tan θ. Draw a
right triangle to help by back substitute.
35) 3 ln  + +
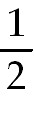 ln ln  +
+
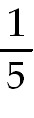 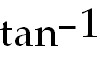
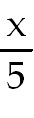 +
C. Use Partial Fraction decomposition. The denominator factors into x( +
C. Use Partial Fraction decomposition. The denominator factors into x(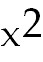 +25).
So the equivalent to the integrand is +25).
So the equivalent to the integrand is  +
+
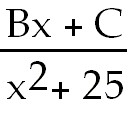 . Find A, B and C and then
integrate. . Find A, B and C and then
integrate.
36) 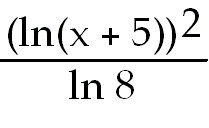 +
C. Rewrite in terms of natural log. Then let u =
x+5 and du=dx. +
C. Rewrite in terms of natural log. Then let u =
x+5 and du=dx.
37) -
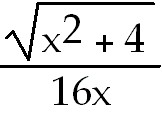 +
C. Use trig substitution with x =
4tan θ and dx =4 +
C. Use trig substitution with x =
4tan θ and dx =4
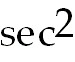 θ d θ. To evaluate the
resulting trig integral, put everything in terms of sin θ and cos θ
and use u-
substitution. Form a right triangle to back substitute so final answer is a
function of x. θ d θ. To evaluate the
resulting trig integral, put everything in terms of sin θ and cos θ
and use u-
substitution. Form a right triangle to back substitute so final answer is a
function of x.
38) 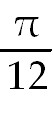 . Rewrite integrand as . Rewrite integrand as 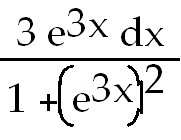 .
If u = .
If u =
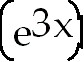 the du =3 the du =3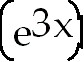 dx.
Match this with the inverse tangent formula. dx.
Match this with the inverse tangent formula.
39) 1. Use l'hopital's rule.
40) let y =
 and take logarithms of both
sides ln y = and take logarithms of both
sides ln y =
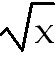 ln x = ln x =

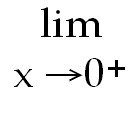 ln y = ln y =
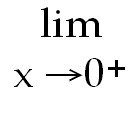 
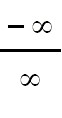 . = . =
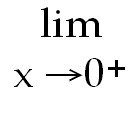  differentiate
differentiate
= 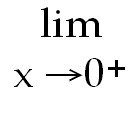 -2 -2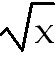 =
0 So
=
0 So 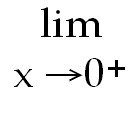  =
=
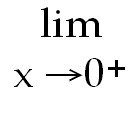 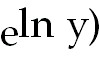 =
=
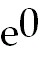 =
1 =
1
41)1. Write as y =
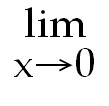 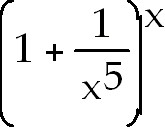 .Take
the natural log on both sides. On the right side use the laws of logs to rewrite
and eliminate the exponent. Rewrite so it is in a .Take
the natural log on both sides. On the right side use the laws of logs to rewrite
and eliminate the exponent. Rewrite so it is in a 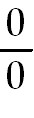 or
or 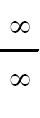 type form so you can use L'Hopital's
rule. Evaluate the limit on the right. That is equal to lny. Solve for y by
taking e to the power on both sides. type form so you can use L'Hopital's
rule. Evaluate the limit on the right. That is equal to lny. Solve for y by
taking e to the power on both sides.
42)Using l'Hopital's rule
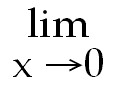 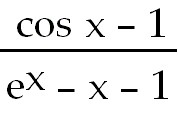
=
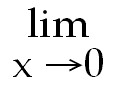 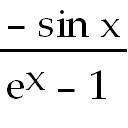 =
=
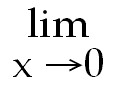  =
=
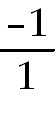 =
-1 =
-1
43)-
 . Use L'hopital's rule twice. . Use L'hopital's rule twice.
| 