|
The answers to the midterm practice are explained following the
test
Farber Math140
- Practice for Midterm
Find the average rate of change of the function over the given interval.
Round to nearest thousandth, if necessary.
1) y
=
4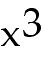 -
6 -
6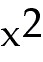 +
8, [-
2, 3] +
8, [-
2, 3]
Complete the table for the function and find the indicated limit.
2) If
f(x) =
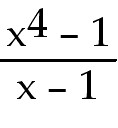 , find lim f(x) x→1 , find lim f(x) x→1
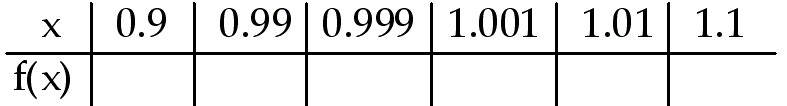
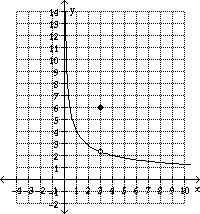
3) Use the graph to estimate the limit of the function.
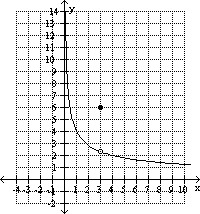 (a) (a)  f(x)
(b) f(x)
(b)  f(x) f(x)
4)
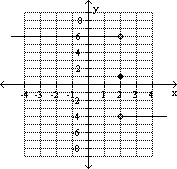
Find 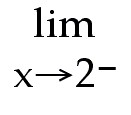 f(x) and f(x) and 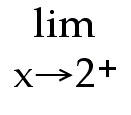 f(x)
and f(x)
and 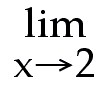 f(x) f(x)
5) Evaluate the limit.
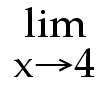 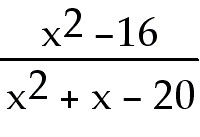
6)
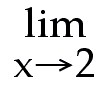
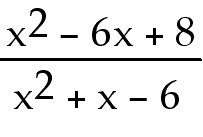
7)  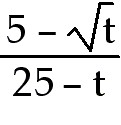
8) Write the
definition of the derivative. Find the derivative of the given function at the
given point using the definition.
f(x) =
3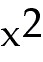 -
2 for a =
-1 -
2 for a =
-1
9) Find the limit, if it exists.
Let f(x) =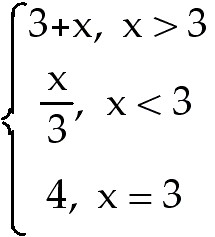
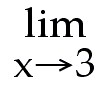 f(x) f(x)
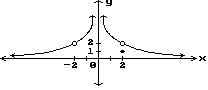
10) Find all points where the function is discontinuous.
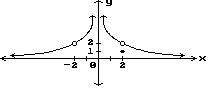
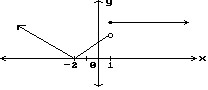
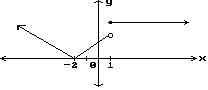
11) Find the x -values
where a) the function is discontinuous b) the function is not differentiable.
Find the intervals on which the function is continuous.
12) y =
13) y =
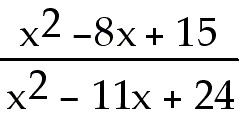
14. Find the equation for the tangent to the curve at the given point.
f(x) =
5x2 +
x; (-4,
76)
Solve the problem.
15. Find the points where the graph of the function have horizontal tangents.
f(x) =
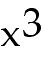 -
21x -
21x
16. Find an equation of the tangent to the curve f(x) =
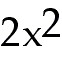 -
2x +
1 that has slope 2. -
2x +
1 that has slope 2.
17. Use the definition to find the function's derivative. Then evaluate the
derivative at the indicated point. g(x)
=
3x2 -
4x, 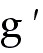 (3) (3)
18. Find the derivative. f(x)
=
4x4 +
3x3 +
6
19. Find an equation for the line tangent to given curve at the indicated
point. y
=
x -
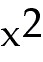 at ( 2, -2) at ( 2, -2)
20. The function s =
f(t) gives the position of a body moving on a coordinate line, with s in meters
and t in seconds, for the given time interval. Use s(t) to find the indicated
quantities.
s =
-
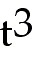 +
2 +
2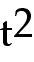 -
2t, 0 ≤
t ≤
2 -
2t, 0 ≤
t ≤
2
Find the body's velocity and acceleration at the end of the time interval.
21. A rock is thrown vertically upward from the surface of an airless planet.
It reaches a height of 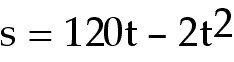 meters in
t seconds. How high does the rock go? How long does it take the rock to reach
its highest point? meters in
t seconds. How high does the rock go? How long does it take the rock to reach
its highest point?
Find the indicated derivative.
22. Find 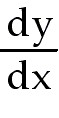 if y = if y =
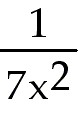 + +
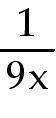 . .
23. y =
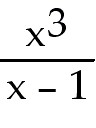
24 y =
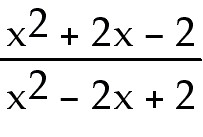
25.Find
the tangent to the curve y =
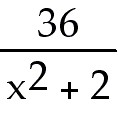 at the point (1, 12). at the point (1, 12).
Find the derivative.
26 y =
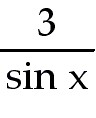 + +
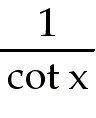
27. r =
18 -
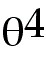 cos θ cos θ
28.Find the indicated derivative.
Find 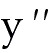 if y =
4 csc x. if y =
4 csc x.
29. Find the derivative of the function.
y =
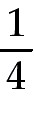 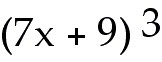 +
+
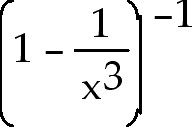
30. r =
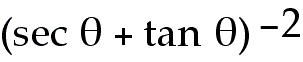
31. f(θ) =
sin  cos cos 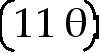
32. y =
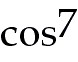 (π t -
13) (π t -
13)
33. q =
cos 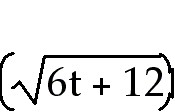
34. h(x) =
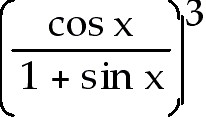
35. y =
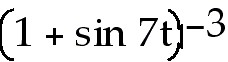
36. Find 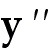 . .
36. y =
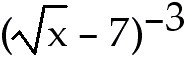
37. y =
4 cot 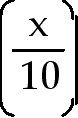
Find
dy/dx by implicit differentiation.
38. x3 +
3x2y +
y3 =
8
39. y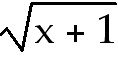 =
4 =
4
40. Find the slope at the indicated point on the given curve.
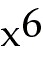 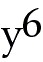 =
64, slope at (2, 1)
=
64, slope at (2, 1)
Find the related rate equation.
41) Suppose
that the radius r and volume V =
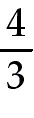 π π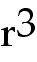 of a sphere are differentiable functions of t. How is dV/dt related to dr/dt?
of a sphere are differentiable functions of t. How is dV/dt related to dr/dt?
42. A product sells by word of mouth. The company that produces the product
has noticed that revenue from sales is given by 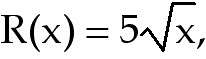 where x is the number of units produced and sold. If the revenue keeps changing
at a rate of
where x is the number of units produced and sold. If the revenue keeps changing
at a rate of 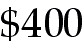 per month, how fast
is the rate of sales changing when 1400 units have been made and sold? per month, how fast
is the rate of sales changing when 1400 units have been made and sold?
43.The radius of a right circular cylinder is increasing at the rate of 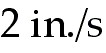 ,
while the height is decreasing at the rate of ,
while the height is decreasing at the rate of 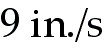 .
At what rate is the volume of the cylinder changing when the radius is 7 in. and
the height is 16 in.? .
At what rate is the volume of the cylinder changing when the radius is 7 in. and
the height is 16 in.?
44. Find the
absolute extreme values of each function on the interval.
F(x) =
3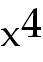 -16 -16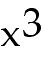 +18 +18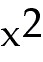 ,
-1
≤
x ≤
4 ,
-1
≤
x ≤
4
45. Find the extreme values of the function and where they occur.
y =
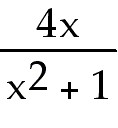
46. Find each critical point and determine if it is a max, min or neither
y =
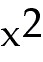 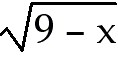
47. y =
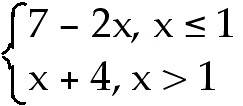
Use analytic methods to find the intervals on which the function is
increasing, decreasing, concave up, and concave down. Also, locate and identify
the local extrema and inflection points.
48. y =
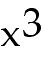 -
27x -
27x

ANSWERS with explanations
Find the average rate of change of the function over the given
interval. Round to nearest thousandth, if necessary.
1)  [- 2, 3] [- 2, 3]
Answer: 22
Explanation: The average rate of change is the change in y
divided by the change in x. To find the change in y, calculate the value of y
for x = 3 which is y = 54 and at x = -2, y = -56. Subtract 54 - (-56) =110.
Divide by the change in x which is 3 - (-2) = 5. The average rate of change is
found by using the slope formula from Algebra.
Complete the table for the function and find the indicated
limit.
2) If f(x) =  ,
find lim f(x) x→1 ,
find lim f(x) x→1

Answer: 3.439; 3.940; 3.994; 4.006; 4.060; 4.641
limit = 4.0
Explanation: Use your calculator and enter the function in Y1.
Evaluate the functions.for each of the given x values. As you get closer and
closer to x = 1 from the right, what is happening to the value of the function?
Now as you get closer and closer from the left, what is happening. If the
function value is getting closer and closer to one y-value, the limit exists and
the y-value is the limit.
Use the graph to estimate the limit of the function.
3)  (a) (a)  f(x)
(b) f(x)
(b)  f(x) f(x)
Answer: (a) about 2.2, (b) ∞
Explanation: The function value (y-value)is getting closer and
closer to 2.2 as x gets closer to3 from the left of 3. . Although the function
is defined at x = 3 f(3) =6, the limit limit is 2.2. The value of the limit does
not depend on the value of the function. (2.2 is approximate)
4)

Find  f(x) and f(x) and  f(x)
and f(x)
and  f(x) f(x)
Answer: 6; -4; does not exist
Explanation: As x gets closer to 2 from the left, the function
gets close to 6. As x gets close to 2 from the right, the function gets close to
-4.  f(x) does not exist since the two one-sided limits
are not equal f(x) does not exist since the two one-sided limits
are not equal
Evaluate the limit.
5)  
Answer: 
Explanation: Direct substitution of x = 4 causes 0 in both the
numerator and zero in the denominator. This is an indeterminate form so you must
rewrite the expression. Factor and reduce. Evaluate the limit in the reduced
fraction since it no longer is undefined at x = 4.
6)  
Answer: - 
Explanation: Direct substitution of x = 4 causes 0 in both the
numerator and zero in the denominator. This is an indeterminate form so you must
rewrite the expression. Factor and reduce. Evaluate the limit in the reduced
fraction since it no longer is undefined at x = 2.
7)  
Answer: 
Explanation: Direct substitution gives 0 in both numerator and
denominator. You can rewrite the expression if you multiply by 1. Use the
conjugate of the numerator as the expression to multiply both numerator and
denominator. Expand and simplify the numerator but keep the denominator in
factored form. Remember you are trying to cancel factors to rewrite.
Write the definition of the derivative. Find the derivative of
the given function at the given point using the definition.
8) f(x) = 3 - 2
for a = -1 - 2
for a = -1
Answer: -6
Explanation: This is a difference quotient and represents the
slope of a curve at a point where the x coordinate is equal to a and the y
coordinate is f(a).
1) f(a + h) = 3 -
2 = -
2 =  + 6ah + + 6ah + . .
2) Subtract f(a) = 3 - 2 from this to get the numerator of the expression. Each term left should have
a factor of h.
- 2 from this to get the numerator of the expression. Each term left should have
a factor of h.
3) Divide by h. The resulting expression will be the difference
quotient. Substitute = -1 to find the value.
Find the limit, if it exists.
9) Let f(x) =
 f(x) f(x)
Answer: Does not exist
Explanation: In a piecewise function, evaluate both one-sided
limits. The limit from the left is 1, the limit from the right is 6. Since these
limits are not equal, the limit does not exist. The graph of this function has a
jump at x =3.
Find all points where the function is discontinuous.
10)

Answer: x = -2, x = 0, x = 2
Explanation: This function has discontinuities at x = 2, x = -2
and x = 0. The discontinuity at x = 0 is an infinite discontinuity. The function
is not defined at x = -2 and at x = 0. Although the function is defined at x =
2, it is not equal to the limit as x approaches 2.
Find the x-values where a) the function is discontinuous b) the
function is not differentiable.
11)

Answer: a) discontinuous at x = 1 b) not differentiable at x =
-2, x = 1
Explanation: A function is not differentiable if the slope from
the right does not equal the slope from the left. This occurs at an corner or
sharp turn. If a function is not continuous it is not differentiable.
Find the intervals on which the function is continuous.
12) y = 
Answer: (-∞,∞)
Explanation: A rational function is not continuous if it is not
defined. This occurs when the denominator is 0. Since no real number will
evaluate to a zero denominator, the function is defined for all reals.
13) y = 
Answer: (-∞, 3), ( 3, 8), ( 8, ∞)
Explanation: A function is not continuous when it is not
defined. A function is not defined when the denominator is 0, so factor the
denominator to find the zeros of the denominator. Find the values that cause the
denominator to = 0. The function *is* continuous at x = 5. A function is defined
as 0 if the numerator is 0 but the denominator is not 0. There is a removable
discontinuity at x = 3 and a non-removable one (a vertical asymptote at x = 8) .
Find the equation for the tangent to the curve at the given
point.
14) f(x) = 5x2 + x; (-4, 76)
Answer: y = -39x - 80
Explanation: First determine the slope. Find the derivative and
evaluate it at x = - 4. . Then use the point slope formula.
Solve the problem.
15) Find the points where the graph of the function has
horizontal tangents.
f(x) =  - 21x - 21x
Answer: (- , 14 , 14 ),
( ),
( , - 14 , - 14 ) )
Explanation: A graph has horizontal tangents when its slope
(derivative = 0. Calculate the derivative and set it = 0. Solve for x.
16) Find an equation of the tangent to the curve f(x) =  - 2x + 1 that has slope 2.
- 2x + 1 that has slope 2.
Answer: y = 2x - 1
Explanation: Find the derivative function. Set this equal to 2
and solve for x. Find the corresponding y value from f (x) and use the
point-slope formula (slope = 2)
Use the definition to find the function's derivative. Then
evaluate the derivative at the indicated point.
17) g(x) = 3x2 - 4x,  (3) (3)
Answer:  (x) = 6x - 4; (x) = 6x - 4;  (3)
= 14 (3)
= 14
Explanation: Use  (x) = (x) =   .
Evaluate and substitute the given value of x. .
Evaluate and substitute the given value of x.
Find the derivative.
18) f(x) = 4x4 + 3x3 + 6
Answer: 16x3 + 9x2
Explanation: Use the power rule on each term. see pages
Find an equation for the line tangent to given curve at the
indicated point.
19) y = x -  at (
2, -2) at (
2, -2)
Answer: y = -3x + 4
Explanation: To write the equation, you need the slope and a
point. The point is given and the slope is determined by the derivative
function.  =1-2x. At x = 2, the slope is -3. =1-2x. At x = 2, the slope is -3.
To writ the equation of the line, use the point - slope formula.
y -  =m(x = =m(x = ) )
The function s = f(t) gives the position of a body moving on a
coordinate line, with s in meters and t in seconds, for the given time interval.
Use s(t) to find the indicated quantities.
20) s = -  + 2 + 2 - 2t, 0 ≤ t ≤ 2
- 2t, 0 ≤ t ≤ 2
Find the body's velocity and acceleration at the end of the time
interval.
Answer: The velocity is 6 m/sec. The acceleration is 8 m/ . .
Explanation: When s = position, velocity is  and acceleration is
and acceleration is  . .
Solve the problem.
21) A rock is thrown vertically upward from the surface of an
airless planet. It reaches a height of  meters in t seconds. How high does the rock go? How long does it take the rock
to reach its highest point?
meters in t seconds. How high does the rock go? How long does it take the rock
to reach its highest point?
Answer: After 30 sec, the rock reaches a maximum height of 1800
m.
Explanation: The rock reaches its maximum height when  = 0. Solve for the value of t and substitute it into the function s.
= 0. Solve for the value of t and substitute it into the function s.
Find the indicated derivative.
22) Find  if y = if y =  +
+  . .
Answer: -  - - 
Explanation: Rewrite using negative exponents. y =  +
+  . Use
the power rule on each term. . Use
the power rule on each term.
Find the derivative.
23) y = 
Answer:  = = 
Explanation: Use the quotient rule. Memorize this and be sure to
learn this formula in the right order.
24) y = 
Answer:  = = 
Explanation: Use the quotient rule. Be sure to memorize this in
the correct order.
Solve the problem.
25) Find the tangent to the curve y =  at the point (1, 12).
at the point (1, 12).
Answer: y = -8x + 20
Explanation: Use the quotient rule to find  .
Evaluate at x = 1. Then use the point slope formula. .
Evaluate at x = 1. Then use the point slope formula.
Find the derivative.
26) y =  + + 
Answer:  = - 3 csc x cot x + = - 3 csc x cot x +  x x
Explanation: This is easier if you rewrite using trig
identities. Know all derivatives for the 6 functions.
27) r = 18 -  cos
θ
Answer:  = - 4 = - 4 co co s
θ +  sin θ sin θ
Explanation: The first term in a constant. Its derivative is 0.
The second term is a product so use the product rule. Watch the + and - signs.
Find the indicated derivative.
28) Find  if y = 4 csc x. if y = 4 csc x.
Answer: 4  x + 4
csc x x + 4
csc x  x x
Explanation: First find  = -4 csc x cot
x.. This is a product. So now use the product rule to find = -4 csc x cot
x.. This is a product. So now use the product rule to find  . .
Find the derivative of the function.
29) y =   +
+ 
Answer:  = =   -
-  
Explanation: Differentiate each term separately. Use the chain
rule on each term. See page 188-190.
30) r = 
Answer:  = - 2 = - 2

Explanation: Use the chain rule. Learn all 6 trig derivatives.
31) f(θ) = sin 
cos 
Answer:  (θ)
= - 11 sin  sin sin  + 2
+ 2 cos cos  cos cos 
Explanation: This is a product so use the product rule here. See
page 188-190.
32) y = 
(π t - 13)
Answer: 
= - 7π  (π t - 13) sin
(π t - 13) (π t - 13) sin
(π t - 13)
Explanation: Rewrite to  . Now use the chain rule with the outside function being the power.
. Now use the chain rule with the outside function being the power.
33) q = cos 
Answer:  = =  sin
sin 
Explanation: Use the chain rule. The outside function is the cos
function and the inside function is  .
Multiply the rates. .
Multiply the rates.
34) h(x) = 
Answer:  (x) = (x) = 
Explanation: Use the chain rule. The outside function is a power
and the inside function is the quotient. Use the quotient rule to find the
derivative of the inside function. Multiply rates.
35) y = 
Answer:  = - 21 = - 21 cos 7t
cos 7t
Explanation: Use the chain rule. The power (- 3 )is the outside
function. The inside function is 1 + sin 7t. Multiply rates.
Find  . .
36) y = 
Answer:  
Explanation: Use the chain rule to find  .
Simplify. Since .
Simplify. Since  is a product, use the product rule to
find is a product, use the product rule to
find  . There are several ways to
express the correct answer. . There are several ways to
express the correct answer.
37) y = 4 cot 
Answer:    cot
cot 
Explanation: First find  . This is a
power. To find . This is a
power. To find  , use the chain
rule. Don't forget to find the derivative of , use the chain
rule. Don't forget to find the derivative of  in each step. This is easier if you rewrite as
in each step. This is easier if you rewrite as  x. x.
Find dy/dx by implicit differentiation.
38) x3 + 3x2y + y3 = 8
Answer: - 
Explanation: Differentiate both sides with respect to x. Don't
forget that each function of y is in turn a function of x so you need the chain
rule. Also, the second term is a product, so use the product rule for that one.
Collect all terms that have  as a
factor to one side and move the rest of the terms to the other side. Factor as a
factor to one side and move the rest of the terms to the other side. Factor  .Finally, divide both sides by the multiplier of
.Finally, divide both sides by the multiplier of  to solve for
to solve for  . .
39) y = 4 = 4
Answer: - 
Explanation: Use the product rule. Differentiate both sides with
respect to x. Don't forget that each function of y is in turn a function of x so
you need the chain rule. Collect all terms that have  as a factor to one side and move the rest of the terms to the other side. Factor
as a factor to one side and move the rest of the terms to the other side. Factor
 .Finally, divide both sides by
the multiplier of .Finally, divide both sides by
the multiplier of  to solve for to solve for  .
.
Find the slope at the indicated point on the given curve.
40)   = 64, slope at (2, 1)
= 64, slope at (2, 1)
Answer: - 
Explanation: Use implicit differentiation to find  .
Use the (2, 1) point for (x, y) .
Use the (2, 1) point for (x, y)
Find the related rate equation.
41) Suppose that the radius r and volume V =  π of a sphere are differentiable functions of t. How is dV/dt related to dr/dt?
of a sphere are differentiable functions of t. How is dV/dt related to dr/dt?
Answer: 
= 4π 
Explanation: Related rates. Assume all variable are functions of
t = time. Differentiate both sides wrt t. Use the chain rule for the right side.
Solve the problem.
42) A product sells by word of mouth. The company that produces
the product has noticed that revenue from sales is given by  where x is the number of units produced and sold. If the revenue keeps changing
at a rate of
where x is the number of units produced and sold. If the revenue keeps changing
at a rate of  per month, how fast is the rate of sales
changing when 1400 units have been made and sold? per month, how fast is the rate of sales
changing when 1400 units have been made and sold?
Answer: $ 5987/month
Explanation: Related rates. The function for revenue is in terms
of x, the u=number of products sold. You are given  =
400. You must find =
400. You must find  when x =
1400. First form the related rates equation containing the two rates of change.
This is done by differentiating both sides of the revenue function wrt t.
Substitute the given values and solve for the unknown rate. See page 208-212 when x =
1400. First form the related rates equation containing the two rates of change.
This is done by differentiating both sides of the revenue function wrt t.
Substitute the given values and solve for the unknown rate. See page 208-212
43) The radius of a right circular cylinder is increasing at the
rate of  , while the height is decreasing at the rate of , while the height is decreasing at the rate of  .
At what rate is the volume of the cylinder changing when the radius is 7 in. and
the height is 16 in.? .
At what rate is the volume of the cylinder changing when the radius is 7 in. and
the height is 16 in.?
Answer: 7π i n.3/s
Explanation: Use V = π h
since the problem involves the volume of a cylinder. You are given  =2
and =2
and  = 9. Find = 9. Find  when r = 7 and h = 16. Form the related rates equation by differentiating wrt t.
The right side involves a product so you will need to use the product rule.
Substitute given values and find the unknown rate.
when r = 7 and h = 16. Form the related rates equation by differentiating wrt t.
The right side involves a product so you will need to use the product rule.
Substitute given values and find the unknown rate.
Find the absolute extreme values of each function on the
interval.
44) F(x) = 3 -16 -16 +18 +18 ,
-1 ≤ x ≤ 4 ,
-1 ≤ x ≤ 4
Answer: Maximum =  ;
minimum = (3, 27) ;
minimum = (3, 27)
Explanation: You are given a closed interval on which the
function is continuous. This means that there are absolute extreme values. An
absolute extreme value can occur at a critical value (where derivative is 0 or
not defined). It could also occur at an endpoint. Find the critical l value(s)-the
endpoints are given. Make a table of values for each possible value of x.
Compare function values to locate the absolute min and absolute max.
Find the extreme values of the function and where they occur.
45) y = 
Answer: The minimum value is - 2 at x = -1. The maximum value is
2at x = 1.
Explanation: Relative extreme values occur when the function
changes direction. This can occur when the derivative is 0 or the derivative
does not exist. Use the quotient rule to find the derivative. Set  =0
and solve. (Checking for undefined values in the domain of the function is a
good habit although that does not affect this problem.) Hint. When you set a
fraction = 0, you can multiply both sides by a non-zero denominator. This
results in numerator = 0. Solve and determine whether values are minimums or
maximums. (Use either first derivative test or second derivative test.) =0
and solve. (Checking for undefined values in the domain of the function is a
good habit although that does not affect this problem.) Hint. When you set a
fraction = 0, you can multiply both sides by a non-zero denominator. This
results in numerator = 0. Solve and determine whether values are minimums or
maximums. (Use either first derivative test or second derivative test.)
Find each critical point and determine if it is a max, min or
neither
46) y =  
Answer:

Explanation: To locate critical points, find the derivative.
Critical points occur when  =0 or is undefined for a
value in the domain in the original function. Use the product rule to
differentiate. In this problem, rewrite the derivative using positive exponents.
This helps identify where =0 or is undefined for a
value in the domain in the original function. Use the product rule to
differentiate. In this problem, rewrite the derivative using positive exponents.
This helps identify where  is not defined. Set is not defined. Set  = 0 to find locations of horizontal tangents. Since you are working with a
fractional equation, multiply by the lcd. For each value you find, tell if it is
a min a max or neither.
= 0 to find locations of horizontal tangents. Since you are working with a
fractional equation, multiply by the lcd. For each value you find, tell if it is
a min a max or neither.
47) y = 
Answer:

Explanation: This function is continuous. There is no place the
derivative is zero, but the derivative is not defined at x = 1. Use the first
derivative test to determine whether is a min or a max or neither.
Use analytic methods to find the intervals on which the function
is increasing, decreasing, concave up, and concave down. Also, locate and
identify the local extrema and inflection points.
48) y =  - 27x - 27x
Answer: increasing at (-∞, - 3) and ( 3, ∞);
decreasing at (- 3, 3); concave down on (-∞, 0); concave up on  local maximum: (- 3, 54); local minimum: (3, -54); inflection point at x = 0
local maximum: (- 3, 54); local minimum: (3, -54); inflection point at x = 0
Explanation: Use the critical numbers from  to analyze the direction of the function. Use the zeros of
to analyze the direction of the function. Use the zeros of  to analyze the type of concavity of the function. There is a point of inflection
where
to analyze the type of concavity of the function. There is a point of inflection
where  = 0 or is undefined and
there is a change in concavity. = 0 or is undefined and
there is a change in concavity.
1) 22
2) 3.439; 3.940; 3.994; 4.006; 4.060; 4.641
limit = 4.0
3) (a) about 2.2, (b) ∞
4) 6; -4; does not exist
5) 
6) - 
7) 
8) -6
9) Does not exist
10) x = -2, x = 0, x = 2
11) a) discontinuous at x = 1 b) not differentiable at x = -2, x
= 1
12) (-∞,∞)
13) (-∞, 3), ( 3, 8), ( 8, ∞)
14) y = -39x - 80
15) (- , 14 , 14 ),
( ),
( , - 14 , - 14 ) )
16) y = 2x - 1
17)  (x) = 6x - 4; (x) = 6x - 4;  (3)
= 14 (3)
= 14
18) 16x3 + 9x2
19) y = -3x + 4
20) The velocity is 6 m/sec. The acceleration is 8 m/ . .
21) After 30 sec, the rock reaches a maximum height of 1800 m.
22) -  - - 
23)  = = 
24)  = = 
25) y = -8x + 20
26)  = - 3 csc x cot x + = - 3 csc x cot x +  x x
27)  = - 4 = - 4 cos
θ +  sin θ sin θ
28) 4  x + 4 csc x x + 4 csc x
 x x
29)  = =   -
-  
30)  = - 2 = - 2

31)  (θ)
= - 11 sin  sin sin  + 2
+ 2 cos cos  cos cos 
32) 
= - 7π  (π t - 13) sin
(π t - 13) (π t - 13) sin
(π t - 13)
33)  = =  sin
sin 
34)  (x) = (x) = 
35)  = - 21 = - 21 cos
7t cos
7t
36)  
37)    cot
cot 
38) - 
39) - 
40) - 
41) 
= 4π 
42) $ 5987/month
43) 7π in. 3/s
44) Maximum =  ;
minimum = (3, 27) ;
minimum = (3, 27)
45) The minimum value is - 2 at x = -1. The maximum value is 2at
x = 1.
46)

47)

48) increasing at (-∞, - 3) and ( 3, ∞); decreasing
at (- 3, 3); concave down on (-∞, 0); concave up on  local maximum: (- 3, 54); local minimum: (3, -54); inflection point at x = 0
local maximum: (- 3, 54); local minimum: (3, -54); inflection point at x = 0
Farber
Practice For Midterm test in Calculus I
Find the average rate of change of the function over
the given interval. Round to
nearest thousandth, if necessary.
1) y = 4
x3- 6
x2 + 8, in the closed
interval [- 2, 3]
Complete the table for the function and find the
indicated limit.
2) If f(x) = 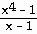 , ,

find lim f(x) x -> 1
3)Use the graph to estimate the limit of the function.
 (a)
lim x->3 (b) lim x
-> 0+ (a)
lim x->3 (b) lim x
-> 0+
4)
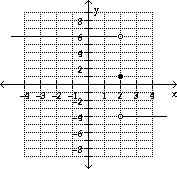
Find
Find
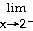 and and
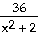 and and
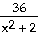
Evaluate the limit.
5)
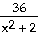
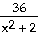
6)
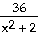
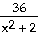
7)
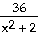
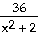
Write the definition of the derivative. Find the
derivative of the given function at the given point using the definition.
8) f(x) =
3
x2 - 2
for a = -1
Find the limit, if it exists.
9)
Find the limit, if it exists.
Let f(x) =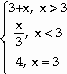
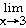 f(x) f(x)
Find all points where the function is discontinuous.
10)
Find the x-values where a) the function is
discontinuous b) the function is not differentiable.
11)
Find the intervals on which the function is continuous.
12) y =
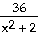
13) y =
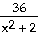
Find the equation for the tangent to the curve at the
given point.
14) f(x) = 5x2
+ x; (-4, 76)
Solve the problem.
15) Find the
points where the graph of the function have horizontal tangents.
f(x) =
x3 - 21x
16) Find an
equation of the tangent to the curve f(x) =
x2 - 2x + 1 that has
slope 2.
Use the definition to find the function's derivative.
Then evaluate the derivative at the indicated point.
17) g(x) = 3x2
- 4x,
Find the derivative.
18) f(x) =
4x4
+ 3x3
+ 6
Find an equation for the line tangent to given curve at
the indicated point.
19) y = x -
x2 at ( 2,
-2)
The function s = f(t) gives the position of a body
moving on a coordinate line, with s in meters and t in seconds, for the given
time interval. Use s(t) to find the
indicated quantities.
20) s = -
t3 + 2t2
- 2t, 0 ≤ t ≤
2
Find the body's velocity and acceleration at the end of
the time interval.
Solve the problem.
21) A rock is
thrown vertically upward from the surface of an airless planet.
It reaches a height of 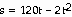 meters in t seconds. How
high does the rock go? How long
does it take the rock to reach its highest point?
meters in t seconds. How
high does the rock go? How long
does it take the rock to reach its highest point?
Find the indicated derivative.
22) Find 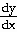 if y =
if y = 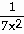 + + 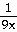 . .
23) y = 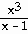
24) y = 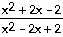
Solve the problem.
25) Find the tangent to the curve y = 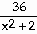 at the point (1, 12).
at the point (1, 12).
Find the derivative.
26) y =
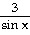 + +
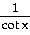
27) r =
18 -
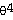 cos θ cos θ
Find the indicated derivative.
28) Find
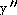 if
y = 4 csc x. if
y = 4 csc x.
Find the derivative of the function.
29) y =
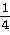
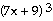 + +
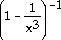
30) r =
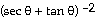
31) f(θ)
= sin
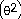 cos cos
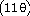
32) y =
cos 7 (π t -
13)
33) q = cos
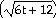
34) h(x) =
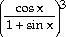
35) y =
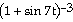
Find
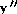 . .
36) y =
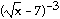
37) y =
4 cot
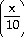
Find dy/dx by implicit differentiation.
38) x3
+ 3x2y + y3 = 8
39) y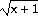 = 4
= 4
Find the slope at
the indicated point on the given curve.
40)
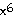
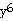 = 64, slope at
(2, 1) = 64, slope at
(2, 1)
Find the related rate equation.
41) Suppose
that the radius r and volume V =
4/3π
r3 of a sphere are differentiable functions of t.
How is dV/dt related to dr/dt?
Solve the problem.
42) A product
sells by word of mouth. The company that produces the product has noticed that
revenue from sales is given by
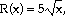 where
x is the number of units produced and sold. If the revenue keeps changing at a
rate of
$400 per month, how fast is the rate of sales changing when 1400 units have been made and sold? where
x is the number of units produced and sold. If the revenue keeps changing at a
rate of
$400 per month, how fast is the rate of sales changing when 1400 units have been made and sold?
43) The
radius of a right circular cylinder is increasing at the rate of
2 in/sec, while the height is decreasing at the rate of
9 in/sec. At what rate is the volume of the cylinder changing when the radius is
7 in. and the height is 16 in.?
Find the absolute extreme values of each function on
the interval.
44) F(x) = 3
x4-16
x3 +18x2, -1
≤ x ≤ 4
Find the extreme values of the function and where they
occur.
45) y =
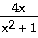
Find each
critical point and determine if it is a max, min or neither
46) y =
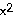
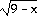
47) y =
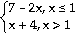
Use analytic methods to find the intervals on which the
function is increasing, decreasing, concave up, and concave down. Also, locate
and identify the local extrema and inflection points.
48) y =
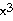 - 27x - 27x
Answers
1) 22
2) 3.439; 3.940; 3.994; 4.006; 4.060; 4.641
or evaluate by algebraic techniques.
limit = 4.0
3) (a)
about 2.2, (b) ∞
4) 6;
-4; does not exist
5)

6) -
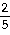
7)
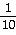
8) -6
9) Does not
exist
10) x = -2, x
= 0, x = 2
11) a)
discontinuous at x = 1 b) not differentiable at x = -2, x = 1
12) (-∞,∞)
13) (-∞,
3), ( 3, 8), ( 8, ∞)
14) y = -39x
- 80
15) (-
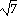 ,
14 ,
14
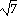 ), ( ), (
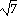 , - 14 , - 14
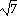 ) )
16) y = 2x -
1
17)
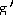 (x) = 6x - 4; (x) = 6x - 4;
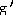 (3) = 14 (3) = 14
18) 16x3
+ 9x2
19) y =
-3x + 4
20) The
velocity is 6 m/sec.
The acceleration is 8 m/
sec2.
21) After
30 sec, the rock reaches a maximum height of
1800 m.
22) -
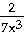 - -
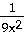
23)
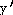 = =
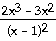
24)
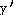 = =
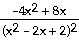
25) y =
-8x + 20
26)
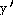 =
- 3 csc x cot x +
sec2x =
- 3 csc x cot x +
sec2x
27)
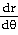 =
- 4 =
- 4
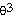 cos θ + cos θ +
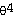 sin θ sin θ
28) 4
csc3x + 4 csc x
cot2x
29)
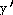 = =
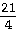
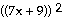 - -
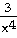
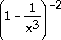
30)
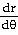 =
- 2 =
- 2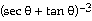
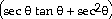
31)
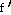 (θ) = -
11 sin (θ) = -
11 sin
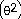 sin sin
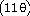 + 2 + 2
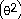 cos cos
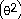 cos cos
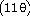
32)
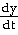 =
- 7π
cox6(π t - 13) sin
(π t - 13) =
- 7π
cox6(π t - 13) sin
(π t - 13)
33)
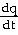 = =
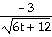 sin sin
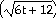
34)
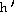 (x)
= (x)
=
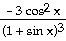
35)
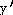 =
- 21 =
- 21
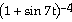 cos
7t cos
7t
36)
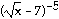
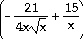
37)
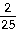
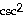
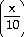 cot cot
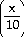
38) -
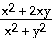
39) -
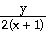
40) -
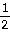
41)
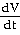 =
4π =
4π
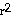
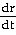
42) $
5987/month
43) 7π
in.3/s
44) Maximum =
(-1 , 37); minimum = (3, 27)
45) The
minimum value is - 2 at x = -1. The
maximum value is 2at x = 1.
46)

47)
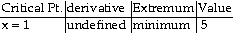
48) increasing
at (-∞, - 3) and (
3, ∞); decreasing at (- 3,
3); concave down on (-∞, 0); concave up on
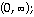 local maximum: (- 3,
54); local minimum: (3, -54);
inflection point at x = 0 local maximum: (- 3,
54); local minimum: (3, -54);
inflection point at x = 0
| 